From polarization of belief to Active learning theory: a diameter approach

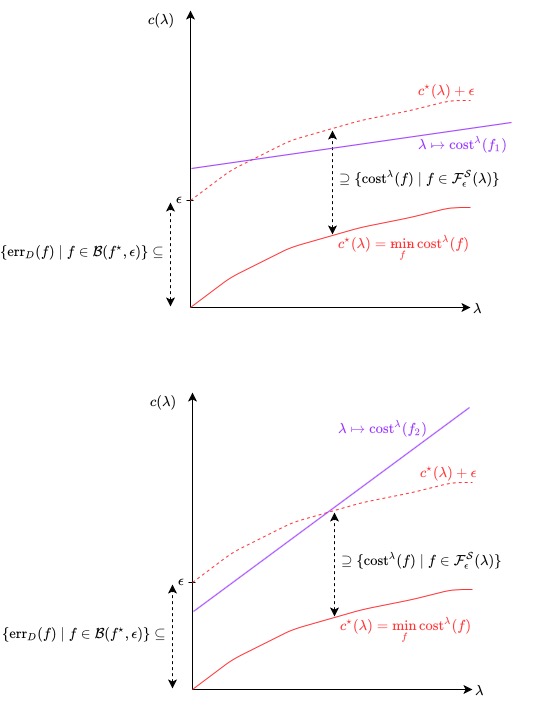
In Haghtalab et al., 2019, polarization of belief is studied through the lens of statistical learning theory. Aside from the innovative ideas, the main theoretical contribution is the introduction of diameter inequalities on an hypothesis class, leveraging only the structure induced by the pseudo metric related to the 0-1 loss. Such diameter is mapped to the maximal disagreement between agents and thus the potential polarization. More precisely, they establish some PAC style bounds on the maximal distance between two penalized ERM hypothesis and study the impact of small modification of the distribution on this distance. With this in mind, this work leverages their framework to further study diameter inequalities under the existence of penalization, without making any assumptions on the structure of the hypothesis space nor on the form of such penalization. Particular attention is given to asymptotic diameter and convergence of empirical and expected approximation sets, called Rashomon Sets. Roughly speaking, we wonder to what extent polarization is robust w.r.t. the penalization? In others words, we analyse the impact of modifications of the penalization associated with hypothesis (i.e.education) on polarization. The second part of the work lays the groundwork of an algorithm whose goal is to introduce bias in the initial distribution in order to reduce maximal diameter, studying an open question of Haghtalab et al., 2019. In particular, some links are established with a line of work in Active Learning community tackling related questions.